[Shader Graph Basics] Dot Product Node (Episode 7)

<Dot Product>

유니티 Shader Graph

-Dot Product (내적 연산) : 벡터의 곱셈은 덧셈뺄셈과 달리 내적(Dot)과 외적(Cross) 2종류가 있다. 벡터의 내적은 Dot 연산이라고도 하며, 두 벡터의 각도의 차이를 숫자로 표현한 것이다. 그냥 각도의 차이를 cos 연산해주면 된다. 그러므로 그 결과는 -1~1의 값이 나온다 (필요하면 Saturate로 0~1로 만들어주기). 이 내적 연산은 라이팅이 아니더라도 두 벡터의 방향이 어떤가를 구할 때 쓰는 공식이다.

 

(대마왕의 유니티 셰이더 그래프 351p)

 

-(cos0 = 1, cos90 = 0, cos180 = -1)

 

-Dot Product Math : 또한 내적은 벡터끼리의 곱셈으로도 표현할 수 있다. Dot Product Node를 자세히 Breakdown 해보면 위와 같다. 연산식으로 표현하면 float3(a,b,c) • float3(x,y,z) = ax + by + cz

그냥 Dot연산 노드를 쓰면 되지 저렇게 연산하지 않아도 된다. 

 

언리얼 Material Editor

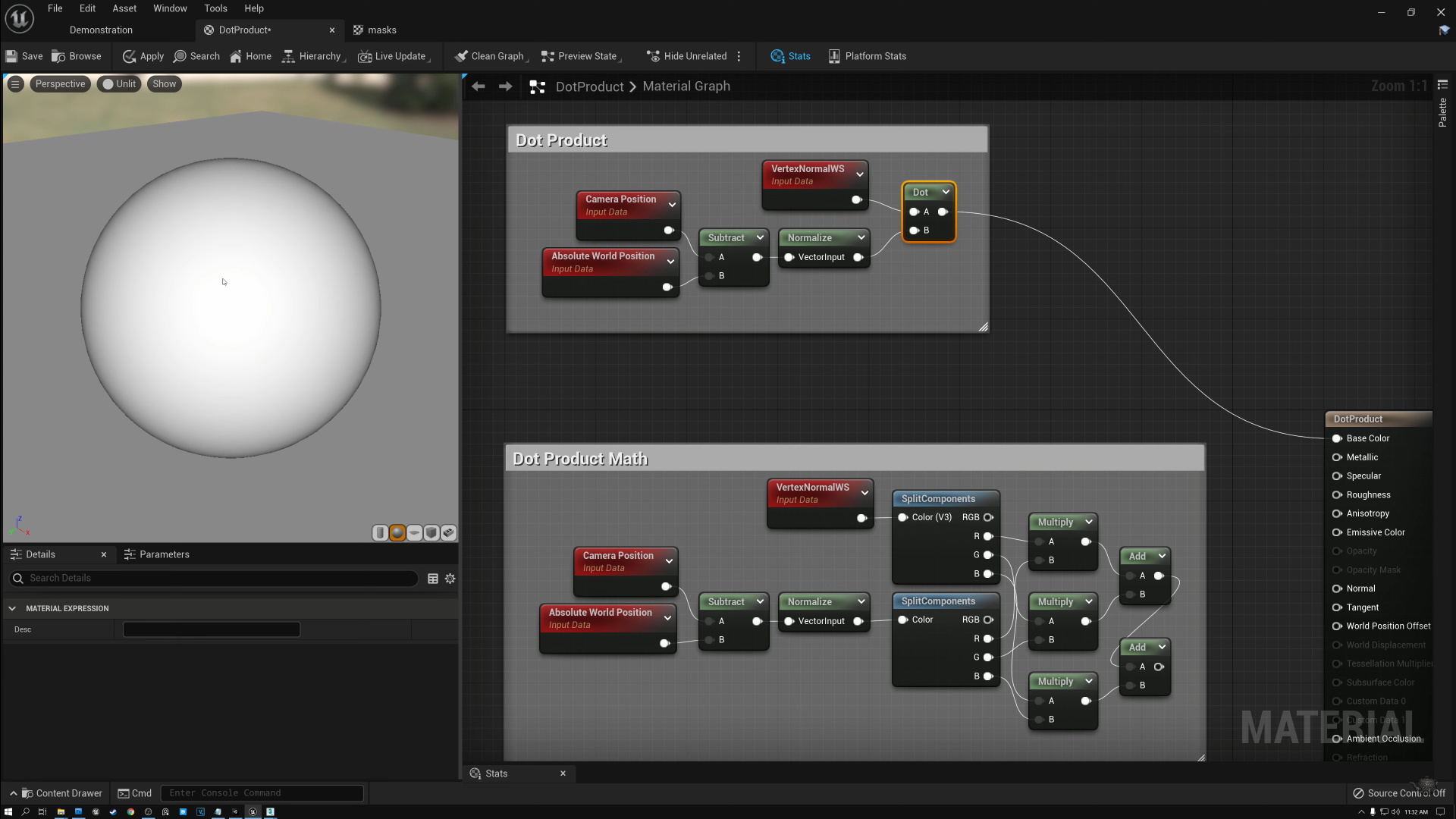
-언리얼에서 Dot Product를 한 예시이다.

 

 

 

<Dot 연산으로 할 수 있는 3가지>

Desaturate a Color (5:56)

1. Desaturate a Color (흑백 만들기)

-RGB 채널을 모두 합치면 색이 되지만 하나하나씩 보면 0~1의 값, 즉 흑백으로 표현할 수 있음. (1,1,0)은 노란색이지만 1(흰) 1(흰) 0(검)인 것처럼. 그러면 R+B+G의 평균값을 구하면 색의 밝기의 평균을 구할 수 있지 않을까. 흑백이란 것은 RGB 각 채널의 숫자가 동일한 것. 그래서 (R+B+G)/3을 해주고 Float1을 Base Color노드의 R,G,B에 각각 연결해주면 됌. 3으로 나누는 이유는 0~1의 값을 3번이나 더했기 때문에 색의 밝기가 원본보다 3배나 밝아짐. 그래서 다시 3으로 나눠줘야 함 (대마왕의 유니티 셰이더 그래프 173p~)

 

-보다 정확하게 하는 법. 빨초파는 휘도(밝기)가 각각 다름. 초록이 가장 휘도가 높고 그다음 빨, 그다음 파임. 밝기 순이 초>빨>파라는 뜻. 이 비율은 (0.2126729, 0.7151522, 0.0721750)이라고 함. 이 휘도의 가중치를 각 RGB에 곱한 후 R+G+B를 해주면 더 정확한 흑백을 만들 수 있음 (대마왕의 유니티 셰이더 그래프 176p~)

 

-그러니깐 위의 방법은 일반 텍스처 샘플과 RGB의 휘도의 가중치 값 (0.2126729, 0.7151522, 0.0721750)을 닷연산하는거랑 똑같은 것임. 닷연산 자체가 float3(a,b,c) • float3(x,y,z) = ax + by + cz 이거니깐. 여기 값에 나누기 3하면 더 정확한가봄. 그리고 위에서 했던것처럼 곱하고 더하고 이렇게 노드를 쭈욱 쓰는 것보다 닷연산 노드 하나만 쓰는게 더 빠르다고 함.

 

Select a Channel (8:05)

2. Channel Selector (채널 선택)

-텍스처에 있는 RGBA 채널 중 하나를 선택하게 하는 기능으로 사용할 수 있음. 플레이 도중 유저가 머티리얼 선택해서 바꿔줘야 할 때 유용하게 쓰일 듯. 텍스처의 RGBA채널에 각각 다른 텍스처들을 넣어놓고 float4 노드와 닷연산. float4에서 그냥 내가 쓰고싶은 텍스처에 1값 넣어두면 됌

 

Compare Two Vectors (14:48)

3. Compare Two Vectors

-두 벡터의 방향이 어떤가를 구할 때 쓰는 것. 위에서 다 설명함

 

-위 프리뷰에서 알 수 있듯이 Camera Vector (= 카메라의 방향 벡터 / 나의 시선)과 오브젝트의 Normal Vector가 서로 마주볼 때 (cos 0) = 흰색(1), Camera Vector (=카메라의 방향 벡터 / 나의 시선)과 오브젝트의 Normal Vector가 직각일 때 (cos90) = 검정(0)이 된다 (cos0 = 1, cos90 = 0, cos180 = -1)

 

-위에서 Camera Vector와 Normal Vector가 서로 마주보고 있는데 180도가 아니라 0도인 이유 :  서로 마주볼 때, 그러니깐 두 벡터의 관계가 180도일 때 가장 밝아야 함. 이때가 가장 밝아야 하는데 cos180를 계산해보면 -1이 되버림. 그래서 일반적으로 연산하기 전 게임 엔진에서 조명 벡터의 방향을 반대로 해준다고 한다. (대마왕의 유니티 셰이더 그래프 354p)

 

 

벡터의 뺄셈 (대마왕의 유니티 셰이더 그래프 349~350p)

-위의 머티리얼 에디터 사진에서 Camera Position - Absolute World Position은 Absolute World Position → Camera Position을 바라보는 방향(벡터)이다. 벡터의 뺄셈이 이런 것임. 위의 그림을 읽어보면 알 수 있음.

 

- A - B는 머리 - 꼬리이다.

 

-위의 머티리얼 그래프를 다시 이어서 설명하면 Camera Position - Absolute World Position을 해서 방향 벡터를 만들고, Normalize해서 0~1의 값으로 만들어준 것이 Camera Vector (=시선 벡터, View Vector)라고 할 수 있다. 이후 Vertex Normal(오브젝트의 버텍스의 방향 벡터)와 Dot 연산을 하면 프리뷰와 같은 결과를 얻을 수 있다.