Pixar In a Box을 보고 정리한 내용이다.
+ 챗지피티한테 물어본 내용도 있어 틀린 내용이 있을 수도 있음
< Image Plane >
-렌즈를 통과한 빛이 이미지를 맺는 곳이다.
-필름 카메라라면 필름이, 디지털 카메라라면 센서가 위치하는 평면이 image plane이 된다.
-디지털 카메라의 센서는 거의 CCD 센서나 CMOS 센서 2종류가 쓰이는데, 웬만해선 요즘은 다 CMOS를 쓴다고 한다.
< Aperture 조리개 >
-Aperture의 사이즈에 따라 빛이 들어오는 양이 달라진다. pinhole 카메라를 생각해보자.
-Aperture가 크면 빛이 더 많이 들어와 밝지만 이미지가 흐려진다. 왜냐면 물체에 한 점을 찍고 그곳에서 오는 빛을 cone형태로 pinhole 카메라의 넓은 구멍에 통과시켜 image plane을 봐보자. 물체에서는 한 점이었던게 image plane에서는 넓은 부분을 차지한다. 그래서 이미지가 블러된 것이다.
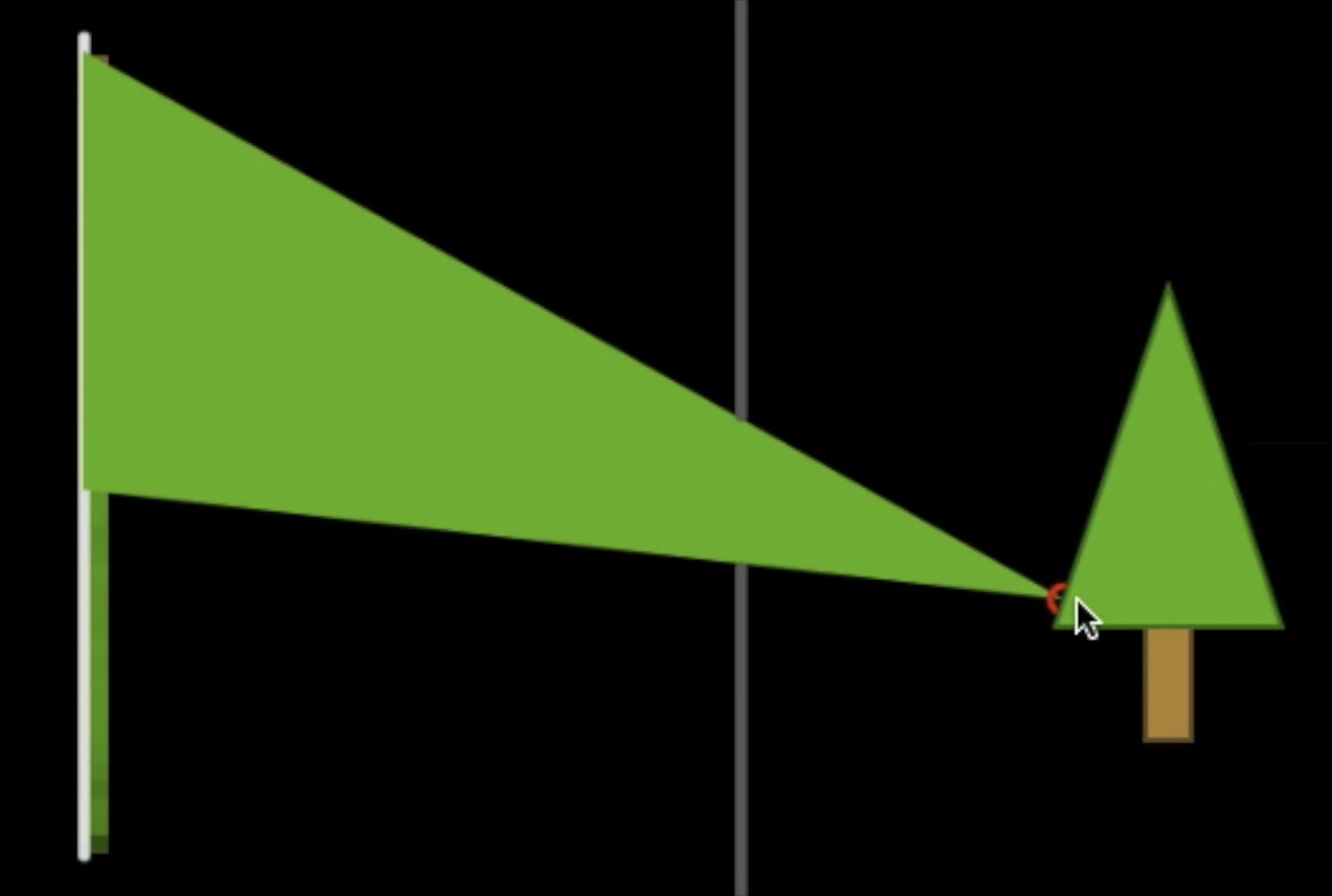
-Aperture가 작으면 빛이 적게 들어와 어둡지만 이미지는 선명하다.
<Focal Distance >
-Aperture과 Image Plane 사이의 거리를 말한다.
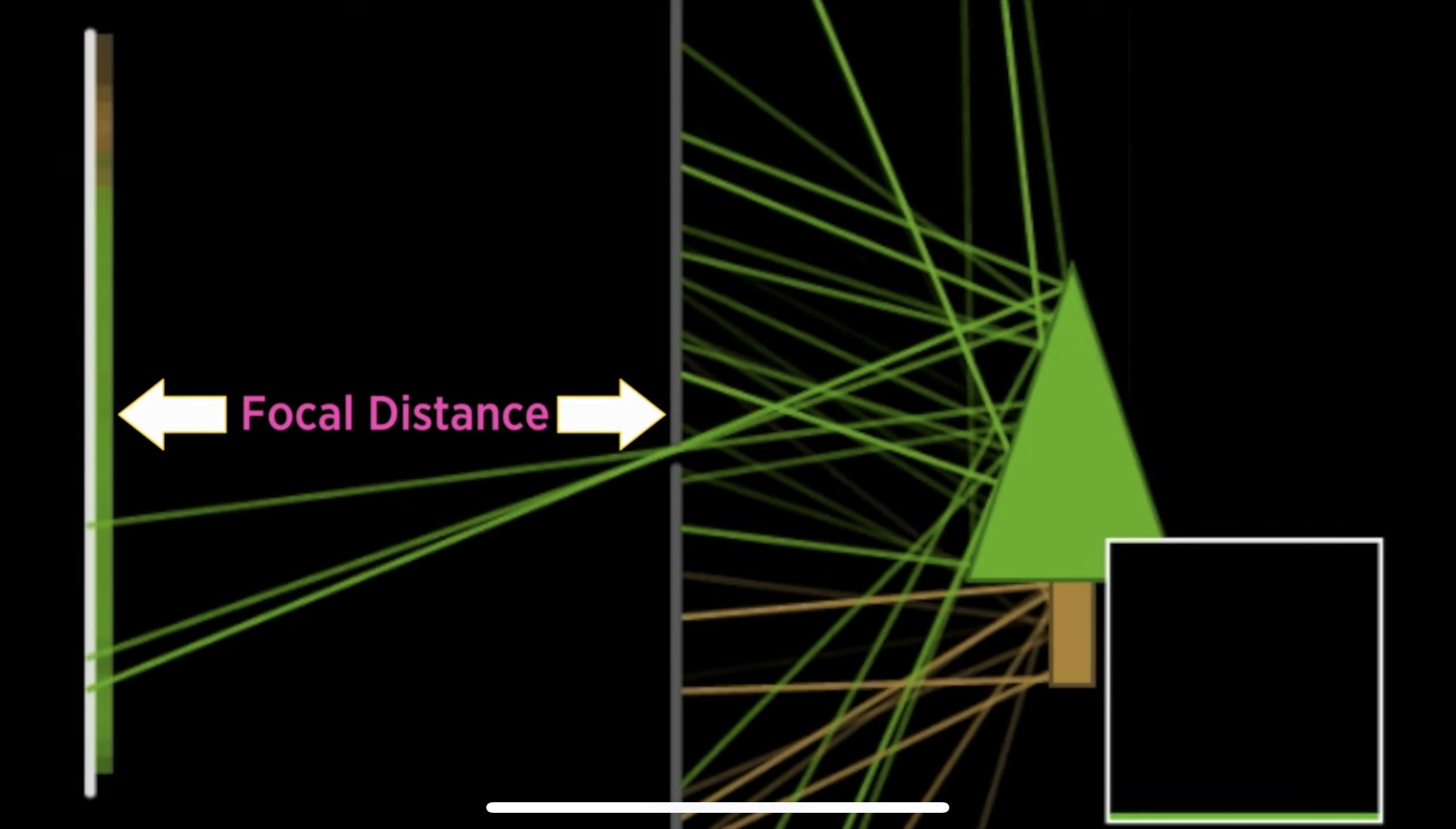
-aperture 사이즈는 그대로 두고 image plane을 조리개 쪽으로 당겨서 핀홀 카메라로 찍어보자. 그러면 물체는 더 조그맣게 보이지만 씬의 더 많은 영역이 찍을 수 있다. 그러니깐 Focal Distance가 짧으면 물체가 조그맣게 보이면서 Field of View가 넓어진다.
-반대로 Focal Distance가 길면 물체가 크게 보이면서 Field of View가 좁아진다. 물체는 더 크게 보이지만 넓은 영역을 찍을 순 없는거다.
-근데 챗지피티에 따르면, Focal Distance(Focus Distance)는 보통 렌즈 ~ image plane의 개념이 아니라 렌즈 ~ 피사체까지의 거리를 일컫는 말이라고 한다. 픽사 강의에서 나온 것은 렌즈가 없는 핀홀 카메라라서 그렇게 용어를 쓴 것 같다고, 렌즈가 있는 카메라에서는 보통 렌즈와 피사체까지의 거리를 나타낸다고 한다. 둘 다 틀린 말은 아니지만 카메라에 따라 사용하는 용어가 조금 다른 것 같다고 한다. 실제 촬영에서는 이 거리 값이 정확한 초점 조절이나 DOF를 정하는데 필요하다고, 포커스 풀러라는 직업이 조절한다고 함. 렌즈 ~ image plane의 거리를 뜻하는 용어는 딱히 없고, 보통 Flange Focal Distance라고 한다.
<Focal Point 초점>
-이제 pinhole 카메라에서 Lens를 도입해보자. 빛은 평행하게 나아간다. 평행한 pinhole을 통과한 빛만이 image plane에 도달한다. aperture이 넓으면 많은 빛이 들어오지만 흐려진다고 했다. 그러나 여기서 lens를 도입하면, 이 평행하게 들어오는 빛을 굴절시켜 한 점으로 모을 수 있다.
-렌즈에 의해 빛이 한 점으로 수렴되는 그 지점을 Focal Point라고 한다. 이 점은 렌즈의 고유한 속성으로, 렌즈의 굴절도에 따라 정해진 고정된 위치이다.
-그러니깐, 렌즈를 하나 정했으면 focal point도 하나의 값으로 정해진다는 것이다.
-또, 초점의 위치는 항상 초점이 맞는 곳이 아니라, 초점은 ‘무한대의 거리에 있는 물체’가 초점이 맞는 지점(=평행하게 들어오는 광선이 한 점으로 모이는 위치)이다. 카메라에 가까이 있는 물체는 focal point에서 초점이 맞게 되는게 아니다.
-그러니깐 focal point에서 항상 초점이 맞게 되는 것이 아니다! 더 자세한 내용은 저 밑에서 설명한다.

-렌즈의 모양이나 곡률에 따라 광선이 얼마나 sharp하게 굴절되는지 결정된다.
-렌즈의 curvature을 증가시키면, 렌즈는 둥그런 타원에 가까워지고, Focal Point는 렌즈에 가까워진다.
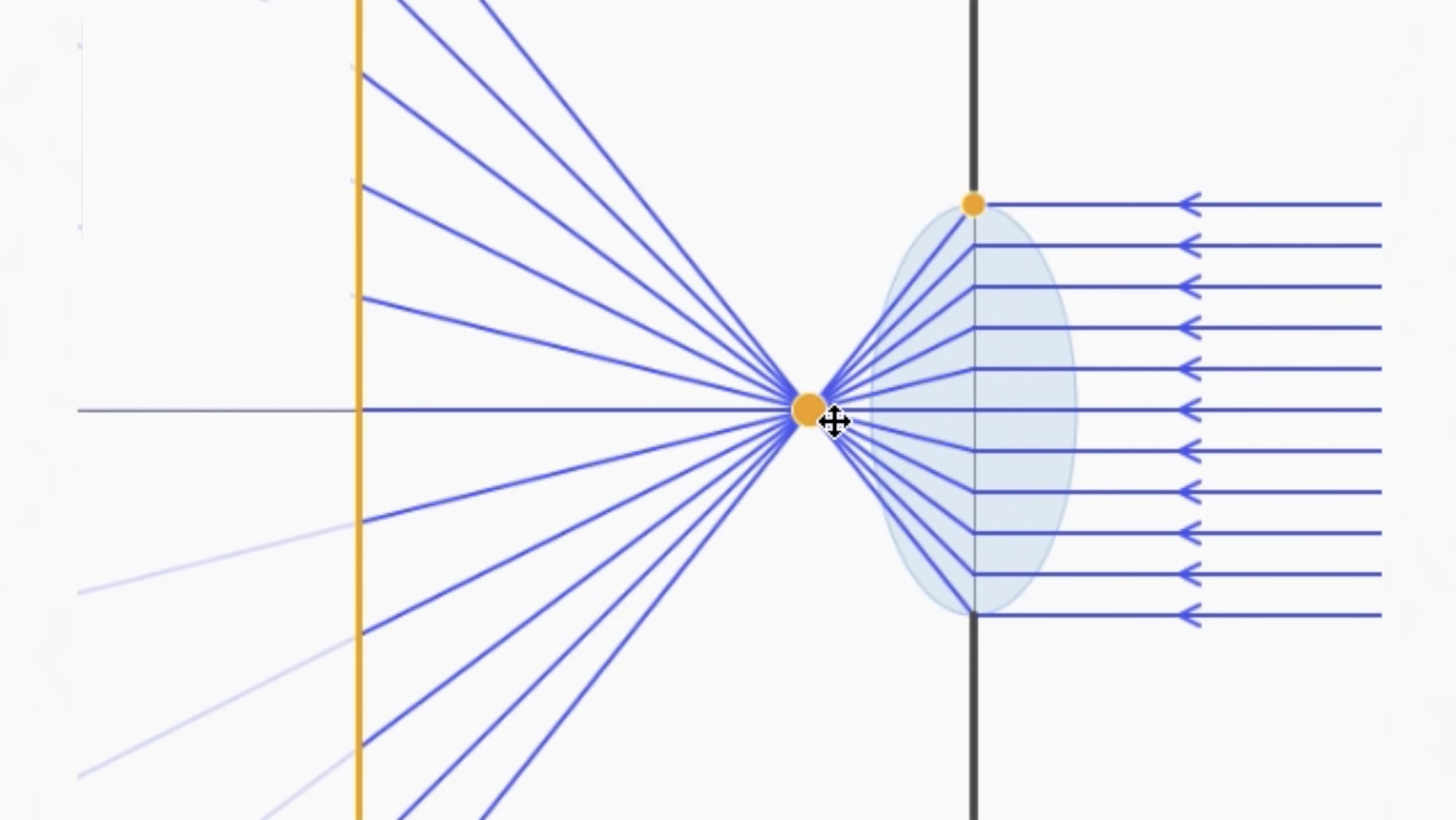
-렌즈의 curvature를 감소시키면, 렌즈는 날카로운 타원이 되고, Focal Point는 렌즈에서 멀어진다.
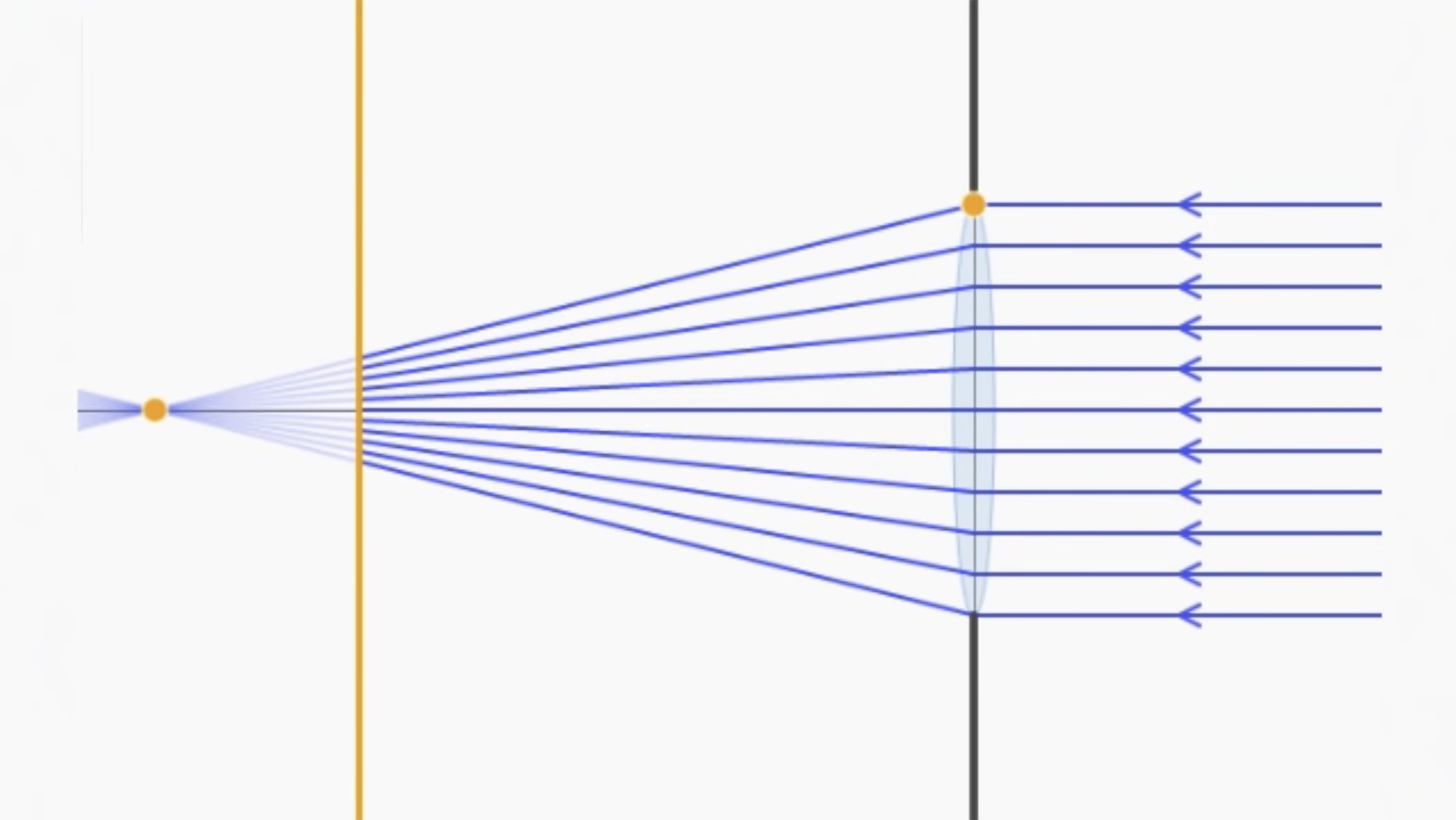
-우리가 원하는 것은 굴절되어 한 점으로 모여진 광선을 image plane에 위치시키는 것이다. 그래야 선명한 이미지를 얻을 수 있다. (평행하게 들어오는 광선일 때)
<Focal Length 초점 거리>
-lens와 image plane 사이의 거리가 어떻든, focal point를 image plane에 위치시키는 렌즈의 모양이나 curvature(굴곡)가 있다
-이렇게 렌즈가 평행한 빛을 모으는 특정한 거리를 Focal Length라고 한다
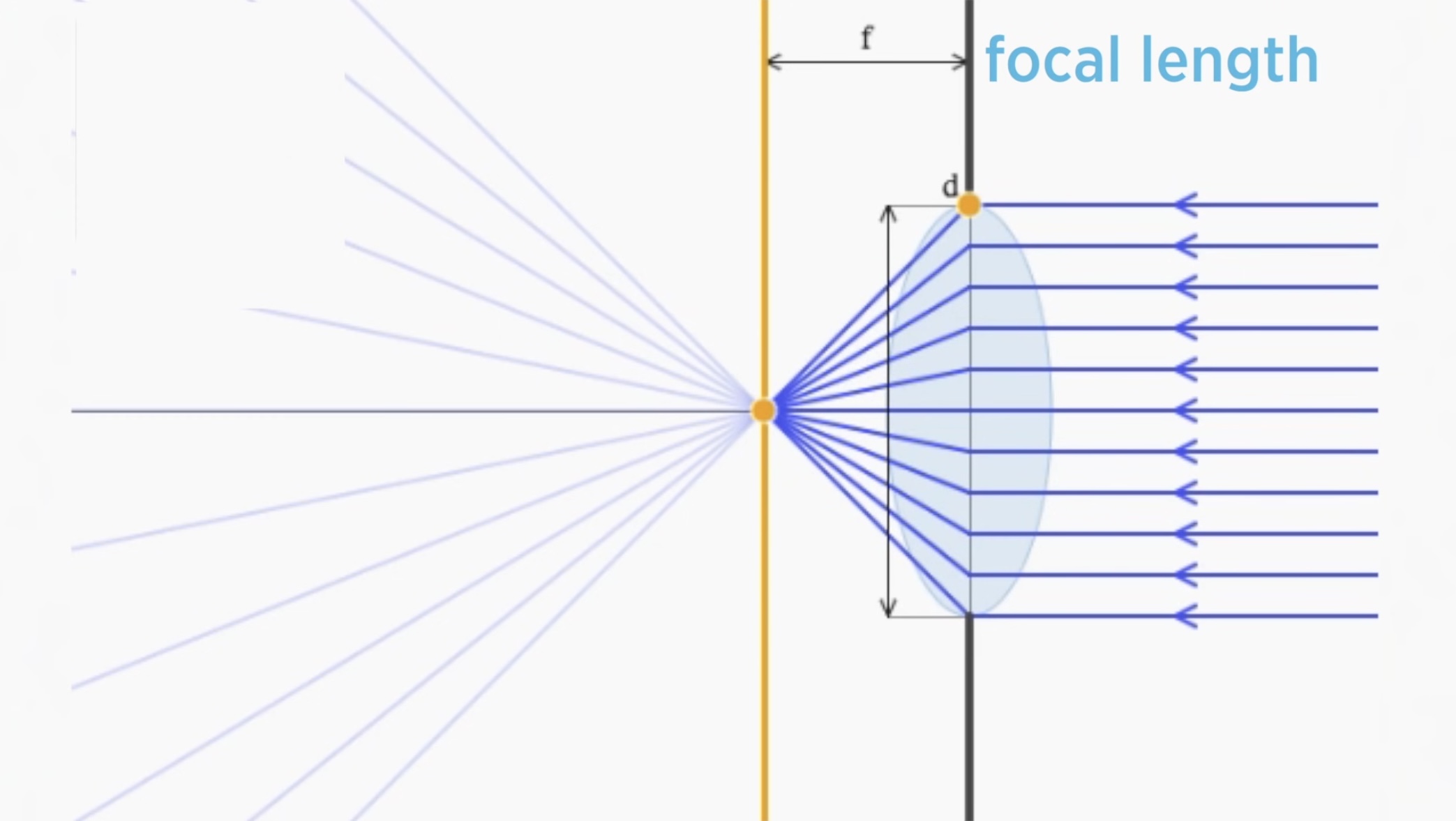
-Focal Length가 짧으면 넓은 FOV(Field of View = 화각)를 갖게 된다. 피사체의 크기는 작아지지만 찍는 시야는 넓어진다. 이게 wide angle lens(광각렌즈)다. 예를 들어 28mm 렌즈가 있다. 여기서 28은 focal length다.
-반대로 Focal Length가 길면 FOV는 좁아진다. 이렇게 aperture에서 먼 곳에 초점을 잡는 렌즈는 long lens(망원렌즈)이다. 예를 들어 120mm 렌즈가 있다. 피사체의 크기는 커지지만 시야는 좁아지는 것이다.
-그렇다면 왜 그럴까? Focal Length가 짧은 렌즈는 두껍고 빛을 많이 굴절시킨다. 반대로 Focal Length가 긴 렌즈는 얇고 빛을 덜 굴절시킨다. 위의 이미지들만 봐도 알 수 있다. 초점에서 모이고 퍼지는 빛의 ray들을 봐보자. focal length가 짧으면 많이 퍼진다. 빛을 더 굴절시켜 빛을 더 넓게 퍼뜨린다. 이게 더 넓은 시야를 가지게 한다. 반대로 focal length가 긴 렌즈는 빛을 덜 굴절시켜 특정한 좁은 영역에 집중시킨다. 그래서 시야가 좁아진다. 결국 각도 때문이다.
* 그러니깐 실제 카메라는 카메라마다 image plane의 위치는 정해져 있다. 렌즈를 바꿀 때마다 focal length가 바뀌는 것임. 만약 35mm 렌즈를 샀으면 focal length는 35mm로 고정. 그렇다면 초점은? 항상 focal point가 image plane 위에 있는 것은 아니다. 렌즈에 따라 고정되어 있는 것도 아니고 조절 가능하다. focal point는 렌즈 자체를 바꾸면서 맞추는 것이 아니라 렌즈의 ‘특정 요소’를 조절하여 focal point를 이동시키는 것이다. 여기서 Focal Point(focus plane)와 Image Plane의 위치를 정확히 맞추면 초점이 맞춰지는 것이다!
디지털의 가상 카메라에서는 Focal Length, Focal Distace, Focal Points를 다 따로따로 조절이 가능해서 헷갈렸지만 위의 내용을 보고 정리하자.
<F-Stop>
-씬의 밝기, 그러니깐 씬에 들어올 빛의 양은 aperture의 지름에 의해 결정된다. 이때 씬의 밝기를 정하는 단위는 조리개의 지름인 mm가 아니라 단위가 없는 f-stop이라는 개념을 이용한다.
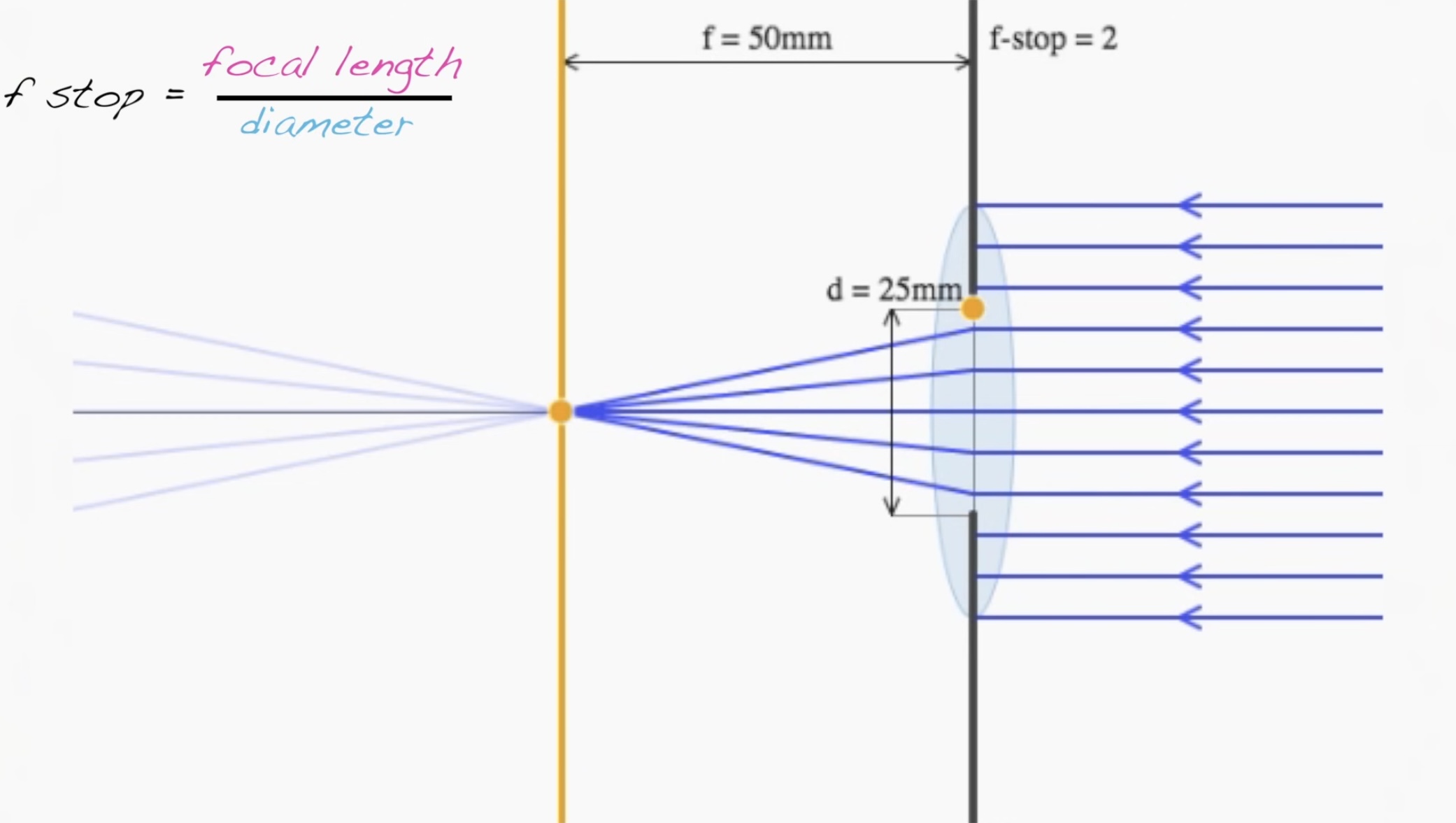
-F-Stop은 Focal Length / Diameter다. 이때 지름은 aperture의 지름이다
-다른 단위도 아닌 fstop을 쓰는 이유는 focal length에 상관없이 빛이 얼만큼 들어오는지 정확히 나타내주기 때문이다
<Depth of Field 피사계 심도>
-lens는 평행한 광선을 하나의 점으로 모으면서 선명한 이미지를 만들 수 있다는 것을 배웠다. 그러니깐 이 말은 image plane이 lens의 focal length에 위치하고 있다면, 매우 멀리 떨어져 있는 물체는 sharp하게 보인다는 것이다. 매우 멀리 떨어져있으면 그 물체에서 카메라로 오는 빛이 평행처럼 느껴질 테니깐 image plane을 렌즈의 focal length에 놓으면 그 물체는 초점이 맞는다.

-그렇다면 이번엔 카메라와 가까운 거리에 있는 오브젝트의 이미지를 만들고 싶다면? 카메라를 움직여서 Joy 캐릭터 바로 앞에 가져다 놔보자. 그다음 Joy에서 한 점을 뽑아서 카메라로 들어오는 광선을 봐보자. 그러면 아까완 달리 빛이 구멍으로 평행하게 들어오지 않고 퍼지는 것을 알 수 있다.
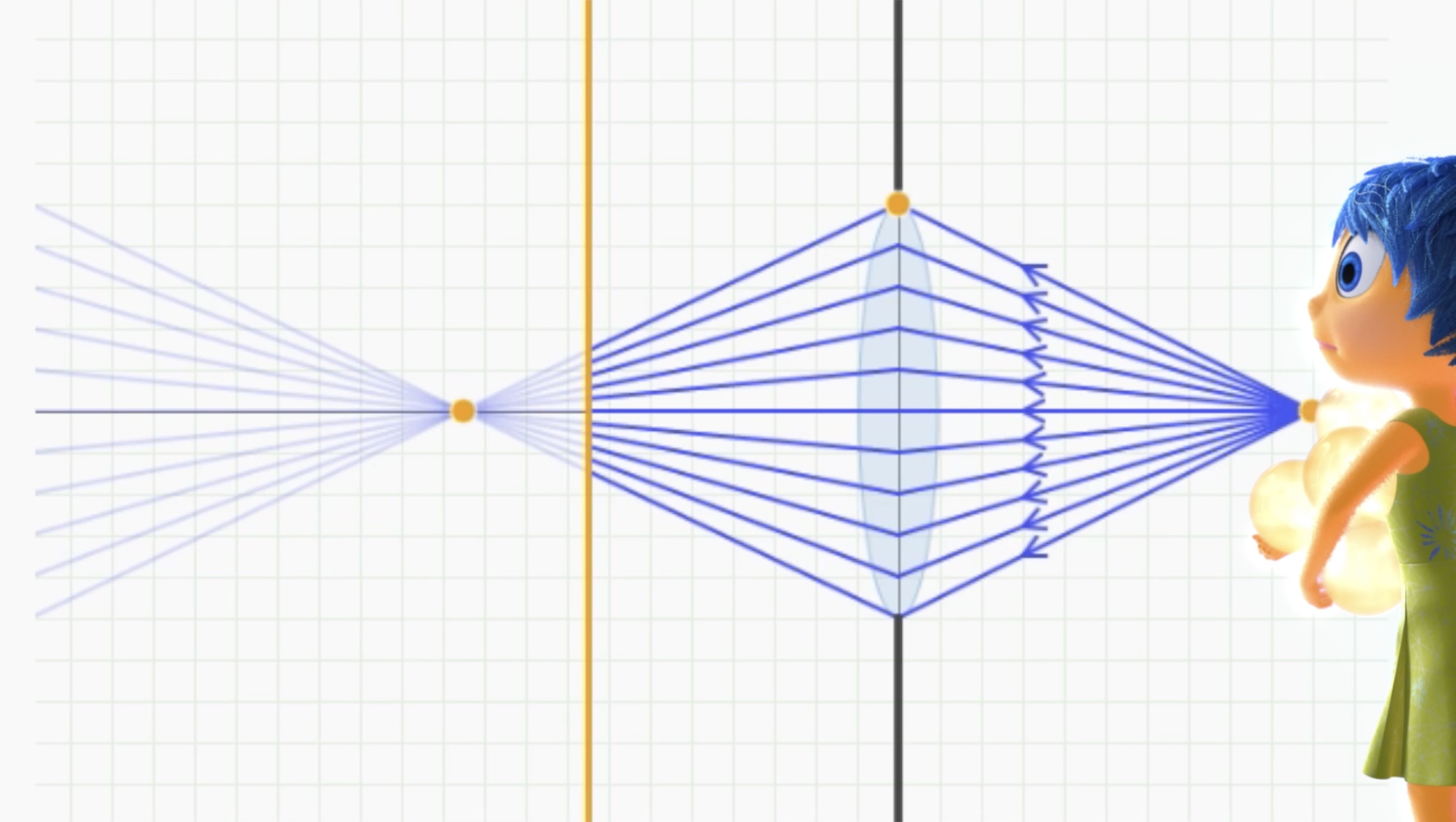
-광선이 렌즈로 평행하지 않고 특정 각도로 들어오기 때문에, image plane보다 살짝 뒤에 초점이 잡힌다. Joy에게서 들어온 광선이 실제 image plane에 부딪힌 곳에서는 한 점으로 모이는 것이 아니라 더 넓은 원 모양으로 퍼져있다. 이렇게 되면 Joy의 이미지가 초점이 나간 것 처럼 보인다.

-더 자세히 보기 위해서 초점이 나간 빛의 사진을 보자. 이렇게 blurry한 원을 Circles of Confusion (착란원)또는 CoC라고 한다.

-초점이 맞지 않은 광선은 image plane에서 이렇게 보인다는 것이다. 초점이 맞게 되면 이 circles of confusion이 너무 작아져서 이미지 상으로는 한 점으로 보이게 되는 것이다. 아래 이미지처럼
-pinhole 카메라에서는 구멍의 크기만 이미지의 blurry/sharpness를 결정한다. 그리고 구 blurry/sharpness는 어느 한 오브젝트에만 적용되는게 아니라 image plane 안에 있는 모든 것이 적용되어 초점이 맞는다.
-그러나 렌즈를 이용하면 전체 씬의 일부분만 초점에 맞게 된다. 이렇게 초점이 맞는 영역이 따로 있고 이 영역을 벗어나게 되면 초점이 맞지 않는다.
-이렇게 초점이 맞게되는 범위를 Depth of Field라고 한다.
-DOF는 1. Focal Length (렌즈 선택) / 2. 카메라와 피사체 사이의 거리 / 3. Aperture(조리개) 크기에 따라 조절할 수 있다.
+ 그런데 왜 초점이 맞는 ‘범위’일까?
: 물론 focal point가 위치한 한 점에서는 ‘완벽하게’ 초점이 맞다. 이론 상으로는 그렇지만 실제로는 초점에서 조금 벗어난 곳에서도 우리가 ‘초점이 맞다’라고 느끼게 된다. 그러니깐 focal point에서 벗어나더라도 허용 가능한 흐림의 범위가 있는 것이다. 그래서 완벽한 초점이 맞는 한 점(Focus Point)만 존재하지만, 우리가 실제로는 그 주변 범위까지도 선명하게 보이는 것처럼 느끼기 때문에 DOF(초점이 맞는 범위)가 생기는 것이다.
1. 초점 거리(Focal Length)에 따라 DOF를 조절할 수 있다.
-망원렌즈의 경우, 초점이 맞는 곳에서 벗어난 곳에서는 빛의 퍼짐 속도(CoC가 커지는 속도)가 빨라서 얕은 심도를 가진다.
-광각렌즈의 경우, 초점이 맞는 곳에서 벗어난 곳에서 빛의 퍼짐 속도(CoC가 커지는 속도)가 완만해서 깊은 심도를 가진다.
+ 왜 그런 것일까?
: 핵심은 빛의 퍼지는 각도가 아니라 빛이 퍼지는 속도(CoC가 커지는 속도) 때문이다.
-광각렌즈는 빛이 더 넓게 퍼진다. 망원렌즈는 빛이 비교적 좁게 퍼진다.
-빛이 퍼지는 각도와 초점이 맞는 지점을 벗어날 때의 흐려지는 속도(=Circle of Confusion이 커지는 속도)는 별개의 개념이다.
-초점거리가 길수록 흐려지는 속도가 빠르다.
-쉽게 말해, 망원렌즈는 물체가 조금만 움직여도 이미지가 크게 변하지만, 광각렌즈는 상대적으로 변화가 작아. 그래서 망원일수록 흐려지는 속도가 빠른 거지.
-이건 그냥 광학 현상이 그렇게 된다. 이를 정리해서 공식으로 만든 것도 있다.

-위 공식을 보면 f(초점 거리)가 길수록 B값이 급격하게 증가하는 것을 알 수 있다.
-어쨌든 초점을 벗어난 지역에서 광각 렌즈는 빛이 퍼지는 속도가 완만하고, 망원 렌즈는 빛이 퍼지는 속도가 빠르다. 광각 렌즈는 완만한 언덕, 망원 렌즈는 가파른 절벽에 비유해서 생각하면 된다.
2. 피사체와 카메라 사이의 거리를 통해서 DOF(심도)를 조절할 수 있다.
-카메라를 피사체에 가까이 위치시키면 초점을 맞출 수 있는 거리가 짧아져 얕은 심도가 된다.
-카메라를 피사체에 멀리 위치시키면 초점을 맞출 수 있는 거리가 증가하여 깊은 심도를 만들어낼 수 있다.
예시를 보며 확인해보자,
-손을 얼굴 가까이 가져와서 보면, 손에 초점을 맞추면 배경이 흐려진다. DOF가 얕아진 것이다.
그런데 손을 멀리 뻗으면, 손도 보이고 배경도 좀 더 또렷하게 보이게 된다. DOF가 깊은 것이다.
+ 왜 피사체와의 거리에 따라 심도가 달라질까?
: 핵심은 DOF는 ‘범위’라는 것과, 빛의 퍼짐에 대해 이해하면 쉽다.
이걸 더 구체적으로 설명하면,
• 피사체가 가까이 있을 때 →
1. 렌즈를 더 강하게 굴절시켜 초점을 가까운 곳에 위치시켜야 한다.
2. 그러면 초점 면(Focus Plane = 초점이 위치한 점을 면으로 표현한 것)에서 벗어난 빛들이 센서(image plane)에 맺힐 때 더 큰 각도로 들어오면서 퍼진다. 위의 이미지를 확인해보자.
3. 초점에서 멀어질수록 빛 퍼짐이 더 커지고, 이것은 빛이 빠르게 퍼진다는 것이다. 빛이 빠르게 퍼진다는 것은 흐려지는 속도가 빠르다는 것과 같다.
4. 초점에서 조금만 벗어나도 빛이 급격하게 퍼져버리면, 허용 가능한 흐림의 범위를 빠르게 벗어나게 된다. 그러니깐 DOF가 얕은 것이다. (허용 가능한 흐림의 범위가 뭔지 모르겠다면 위의 [+ 왜 초점이 맞 는 ’범위‘일까?]를 먼저 읽어보자)
반대의 경우도 이해할 수 있을 것이다.
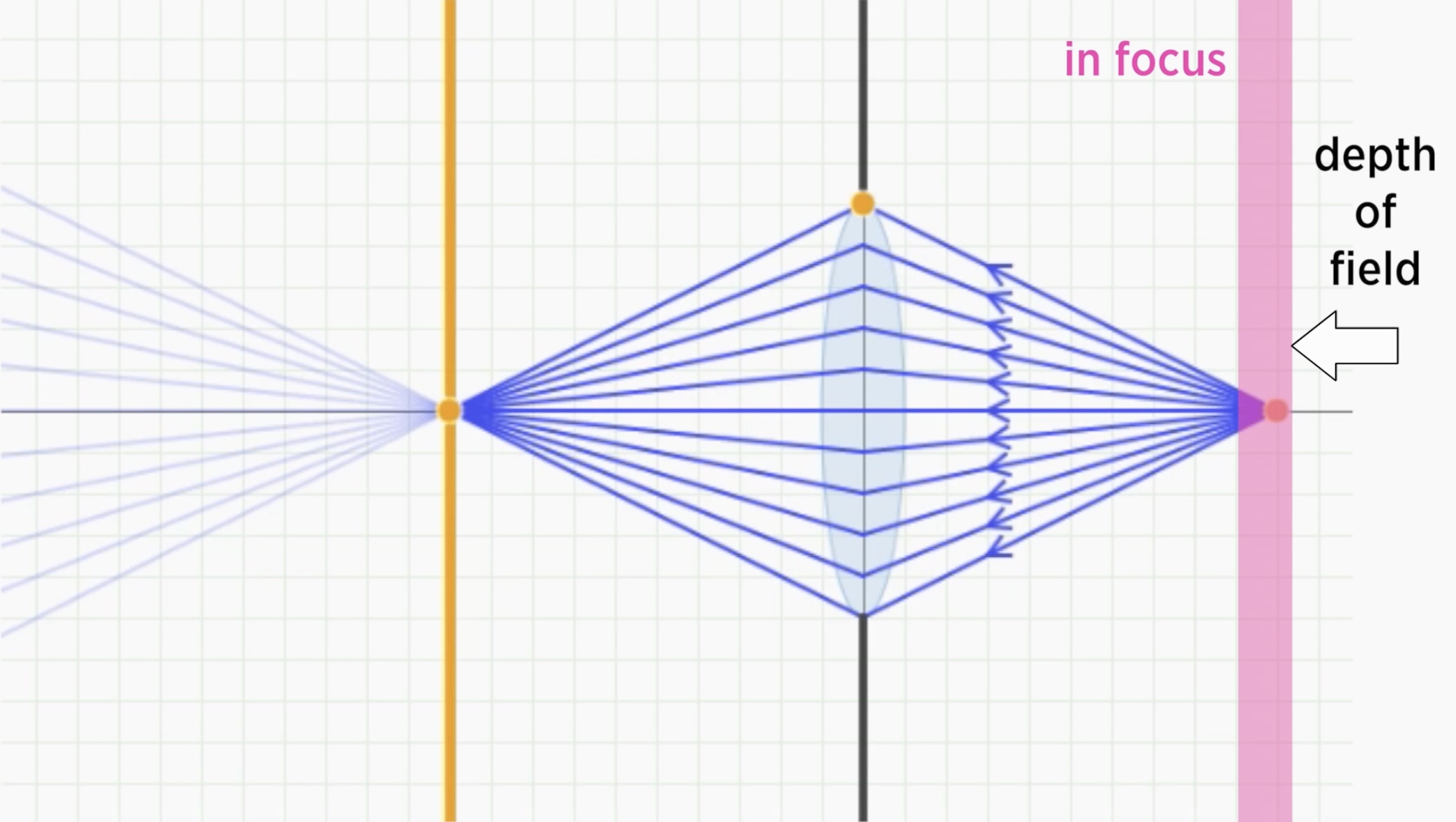
3. 조리개 크기에 따라 DOF를 조절할 수 있다.
-Aperture 크기가 줄어들면 F Stop은 커진다. 그리고 DOF는 넓어진다. 또 이미지가 선명한 것에서 흐려지는 전환이 되게 부드럽다. 이런 것을 Deep Depth of Field (깊은 심도)라고 한다.
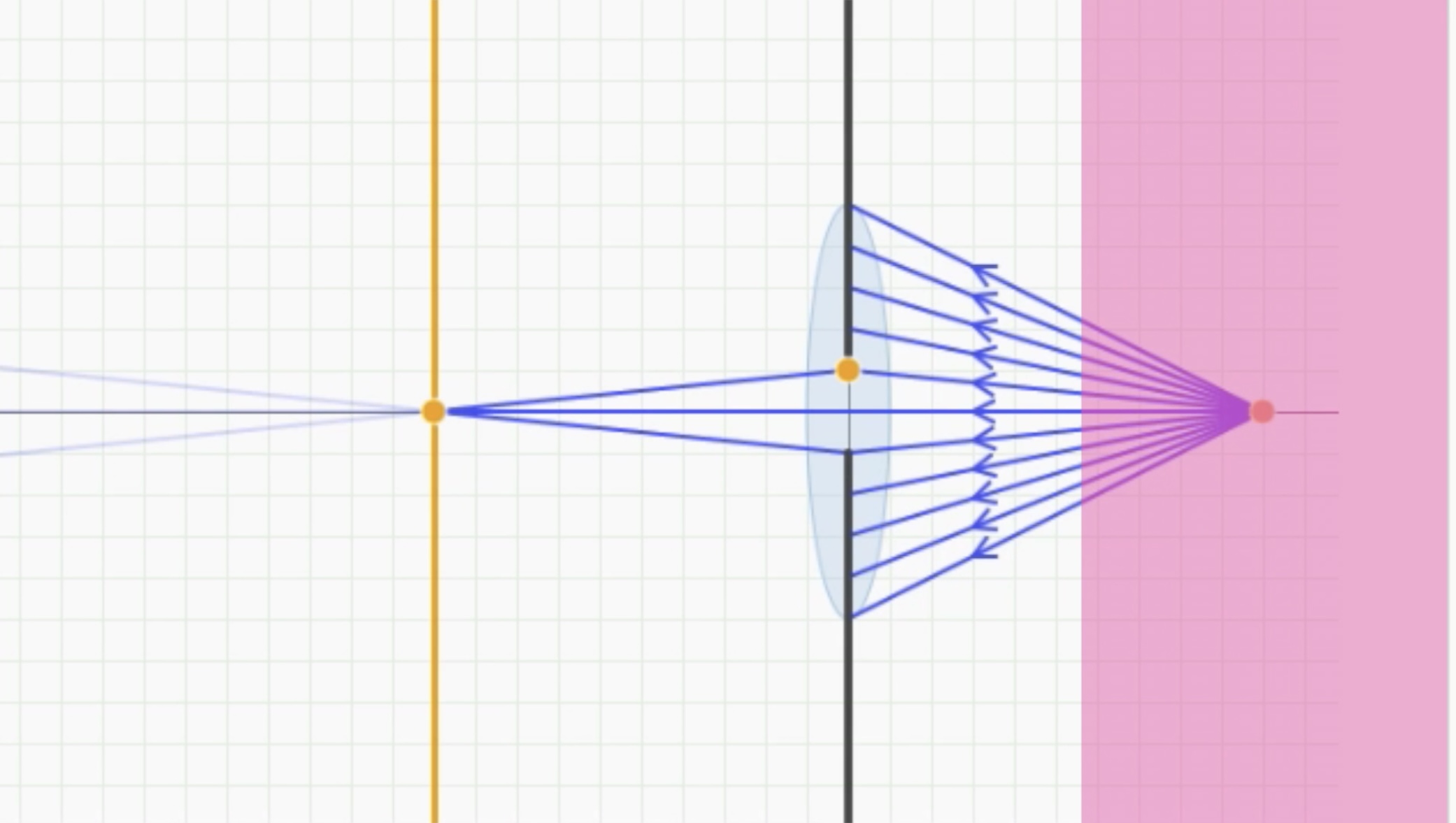
-반대로 aperture 크기가 커지면 DOF는 좁아진다. 그리고 선명함에서 블러로 되게 급격하게 전환된다. 이것을 Shallow Depth of Field(앝은 심도)라고 한다. 씬에서 아주 작은 영역에서만 초점이 맞는 것이다

-정리하자면, 얕은 DOF를 만들고 싶으면 Aperture를 크게 하거나 F Stop을 작게 하면 되고, 깊은 DOF를 만들고 싶으면 Aperture를 작게 하거나 F Stop을 크게 하면 된다.
+ 왜 Aperture 크기에 따라 DOF가 달라지는가?
빛의 굴절과 초점의 원리같은 물리학적인 면을 살펴봐야 한다. 이것도 결국 ‘빛의 퍼짐’과 관련해서 설명할 수 있다.
- Aperture가 클수록(좁은 F-stop) 카메라 렌즈로 들어오는 빛의 양이 많아지고, 빛이 센서를 향해 더 넓게 퍼져서 들어옵니다.
- 이로 인해 피사체 이외의 초점이 맞지 않는 부분(초점면 밖의 영역)에서 빛이 더 넓게 퍼지며 배경과 전경이 더 흐릿해집니다. 즉, 얕은 DOF를 만듭니다.
- 반대로 Aperture를 작게(넓은 F-stop) 설정하면 빛이 더 좁게 집광됩니다. 이는 초점면 밖의 빛의 퍼짐을 줄여 더 많은 영역이 초점이 맞는 것처럼 보이게 만들어 깊은 DOF를 형성합니다.
- 또 다른 이유로, Aperture에 따라 빛이 들어오는 크기가 달라지면서 빛의 경로가 제한되는 측면도 있다.
- Aperture가 클수록 빛이 통과할 수 있는 각도가 넓어지고, 초점면에 도달하지 못하는 빛(흐릿한 빛)의 양이 늘어납니다. 이로 인해 초점면 이외의 영역이 더 크게 흐려지는 것입니다.
- Aperture가 작을 경우, 빛의 각도가 좁아지고 초점면에 가까운 경로만 허용되기 때문에 초점이 맞는 범위가 확장됩니다.
챗지피티의 답변을 정리한 것이지만 답변의 출처는 이러하다고 한다.
-Cambridge in Colour (https://www.cambridgeincolour.com)
-Photography Life (https://photographylife.com)
-Khan Academy
-그러니깐, 프레임 안에 피사체를 담을 때 원하는 크기가 있을 것이다. 이때, 멀리 있는 것을 줌으로 당겨서 원하는 크기로 만들건지, 아니면 카메라를 피사체에 직접 가까이 다가가서 원하는 크기로 만들 것인지 선택하게 된다. 만약 멀리 있는 것을 줌으로 당긴다면 깊은 심도로 찍힐 것이고, 피사체에 직접 가까이 다가간다면 얕은 심도로 찍힐 것이다.
<어디에서 focus가 맞게 되는 것인가>
-Depth of Field에서 벗어나게 되면 blurry 해지면서 오브젝트가 흐린 원형의 모양으로 바뀐다. 이 흐린 원을 Circle of Confusion(착란원) 이라고 한다.
-그래서 어디에서 focus가 맞게 되고 DOF에서 벗어날 시 Circle of Confusion의 크기는 어떻게 되는가? 수학적으로 알아보자
-다시 pinhole 카메라로 돌아와서 수식을 살펴보자.
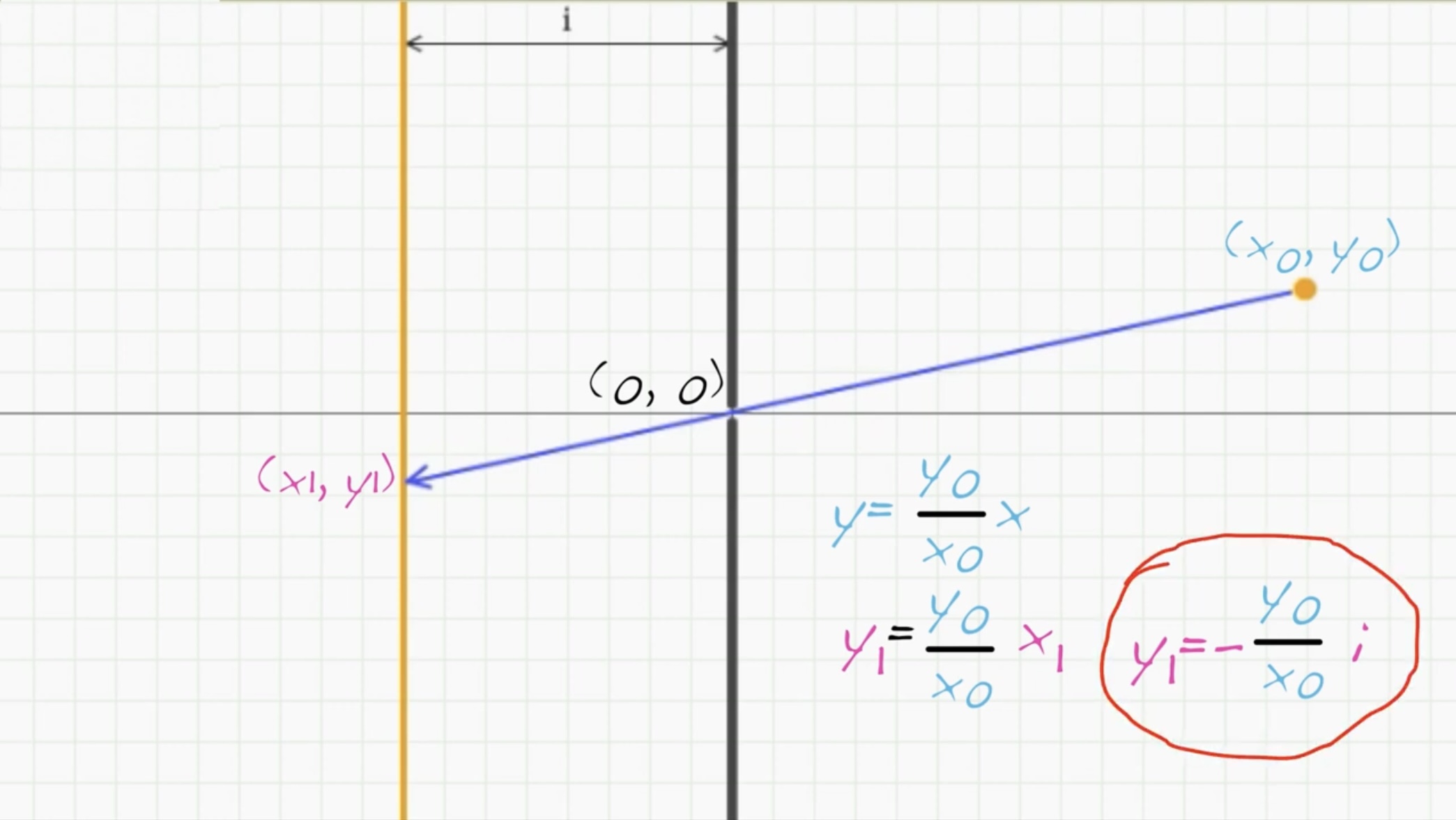
- 원점 (0,0)이 Aperture의 위치이고
- (x0, y0)은 오브젝트의 위치,
- i는 aperture과 image plane 사이의 거리인 Focal Distance,
- (x1, y1)은 오브젝트의 위치에서 빛이 pinhole 카메라의 aperture을 통과하여 image plane에 닿은 위치이다.
이때 우리가 알고싶은 것은 (x1, y1)의 위치는 어디인가? 이다.
이것은 기울기를 이용해서 구할 수 있다. 저 직선의 기울기는 y0/x0이고 이를 이용하여 식을 써보면
y = y0/x0 * x
이에 (x1, y1)을 대입해보면 y1 = y0/x0 * x1인데 x1은 -i와 같으니깐 y1 = -y0/x0 * x1
위 사진을 보면 y0는 원래 양수이다. 그러나 해당 점이 image plane 위에서는 음수에 해당한다. 이것이 pinhole 카메라로 찍었을 때 Image Flip이 일어나는 이유이다!
-이제 pinhole 카메라 말고 lens가 들어간 카메라를 봐보자.
-물체가 렌즈로부터 아주 멀리 떨어져 있을 때, 아래
그림처럼 물체로부터 들어오는 빛은 평행하게 들어올 것이다. 그리고 이 빛은 렌즈에 의해 굴절되어 한 점으로 모일 것이다. 이 점을 Focal Point라고 하고, 렌즈로부터 focal point까지의 거리를 Focal Length라고 한다는 것을 이미 배웠다.
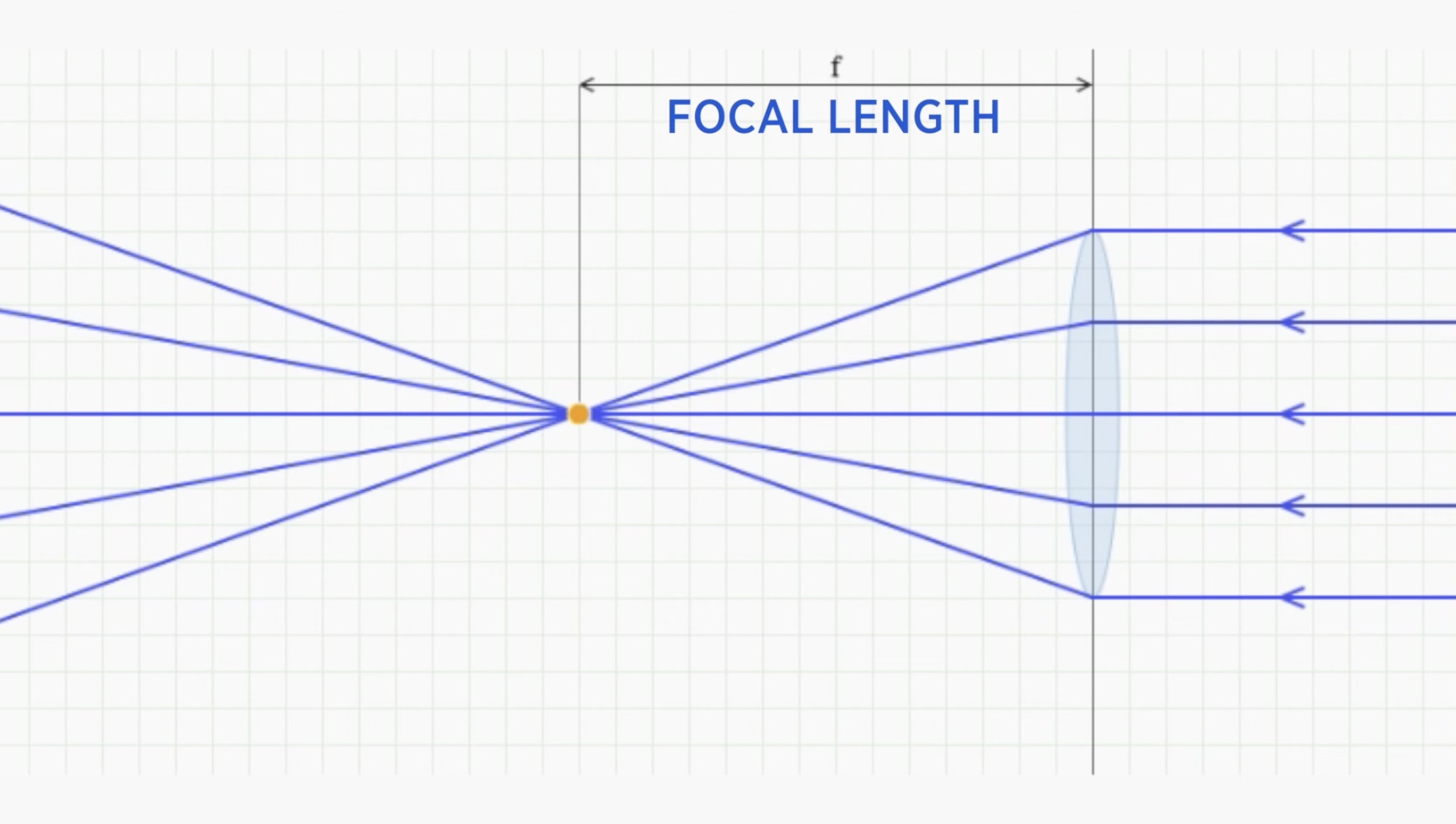
-그러면 이제 렌즈로부터 아주 먼 물체 말고 렌즈 근처에 가까이 놓여져있는 물체에 대해 생각해보자. 이 물체는 어디에서 초점이 맞게 될까?
-즉, image plane을 어디에 놓아야 이미지가 sharp하게 보일까?
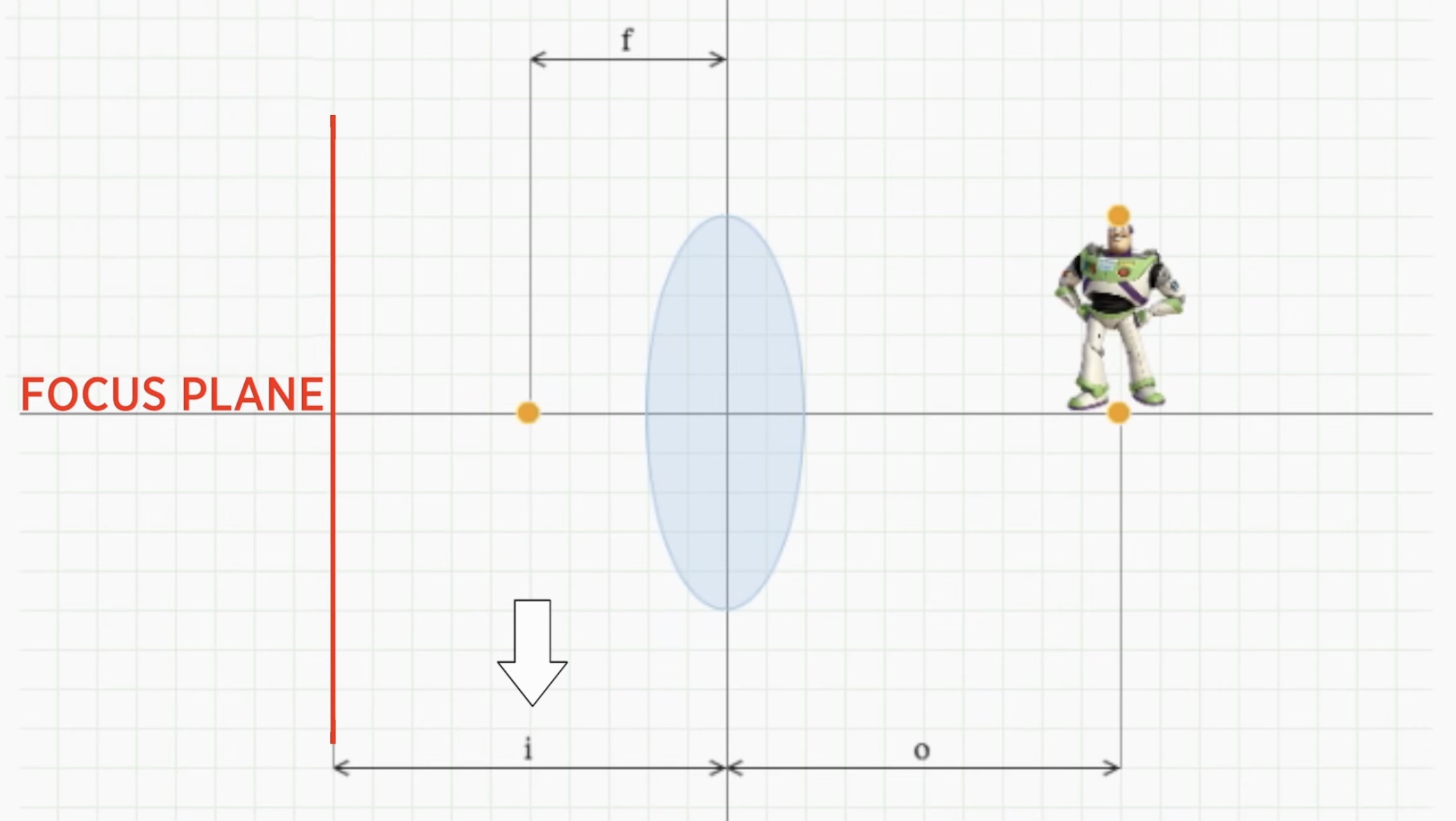
- f는 렌즈의 focal length다.
- o는 우리가 초점을 맞추고 싶은 물체까지의 거리이. 다. 물체에서 렌즈까지의 거리이다.
- i는 물체의 초점이 맞게 되는 렌즈로부터의 거리이다. 여기를 focus plane이라고 부르자. 즉, i는 초점이 맞는 위치를 결정하기 때문에 그곳에 image plane을 놓으면 되는 것이다. 그러니깐 렌즈에서 image plane까지의 거리가 된다.
-우리는 f와 o를 이용하여 i를 구하면 되는 것이다.
+ 그럼 그냥 f의 위치에 image plane이 있으면 초점이 맞는거 아닌가?
: 아니다! 초점/초점거리는 항상 초점이 맞는 곳/거리가 아니라, ‘무한대의 거리에 있는 물체’가 초점이 맞는 점/거리이다.
그림처럼 피사체가 무한대의 위치가 아니라 카메라 가까이에 위치한 물체는 초점이 맞는 위치(i)가 f보다 멀어져야 한다! 그냥 광학 현상이 그렇게 된다. 그걸 공식으로 정리한거고.
: 또 focal point의 위치는 focus plane의 위치가 아니다! 위에서 말했듯이 focus는 무한대의 거리에 있는 물체가 초점이 맞는 지점인 것이다. 우리가 찍는 물체는 무한대가 아니니깐 초점거리(f)와 i는 다를 수도 있는거다.
그렇다고 초점이 f와 i 두 군데에서 맺히는 것은 아니다. 항상 focus plane 위에서 초점이 맞게 된다. 즉, focus(초점) 자체는 특정 지점에서 빛이 모이는 개념이고, 그 빛이 모여서 이미지가 선명하게 맺히는 곳이 focus plane이다.
그래서 초점이 두 군데에서 따로 맞는 게 아니다!
-이걸 구하기 전에, 렌즈가 어떻게 빛을 굴절하는지 알아야한다. 굴절은 되게 복잡한데, 스넬의 법칙으로 알아볼 수 있다. 근데 뭐 지금은 필요없다. 좀 더 간편화된 Thin Lens Approximation (얇은 렌즈 방정식)으로 알아볼 것이다.
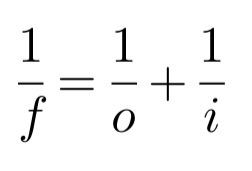

-이 방정식에 의하면, 렌즈의 중심을 지나는 광선은 전혀 굴절되지 않고 직선으로 나아간다. 이 광선을 Medial Ray(내측선)라고 부른다.
-그러나 렌즈의 중심을 지나지 않고, 평범하게 렌즈를 지나가며 굴절되는 Parallel Ray(걍 평행한 광선)는 알고있듯이 굴절되어 Focal Point(초점)를 지나게 된다.
-렌즈에서부터 이 두 종류의 광선인 Medial Ray와 Parallel Ray가 교차하는 지점까지의 거리를 i로 보면 된다! 여기서 초점이 맞게 되는 것이다
-렌즈 방정식에 따르면, 예를 들어 버즈 머리에서 한 점을 잡고 여기서 교차점을 찾아 i를 찾는다. 그리고 버즈 머리에서 출발한 모든 광선은 결국 저 교차점을 지나게 된다는 것이다.
-헷갈렸어서 적어두는건데 이건 렌즈에 관한 것이므로 조리개 크기가 바뀐다고 해서 저 교차점의 위치가 변하진 않는다!

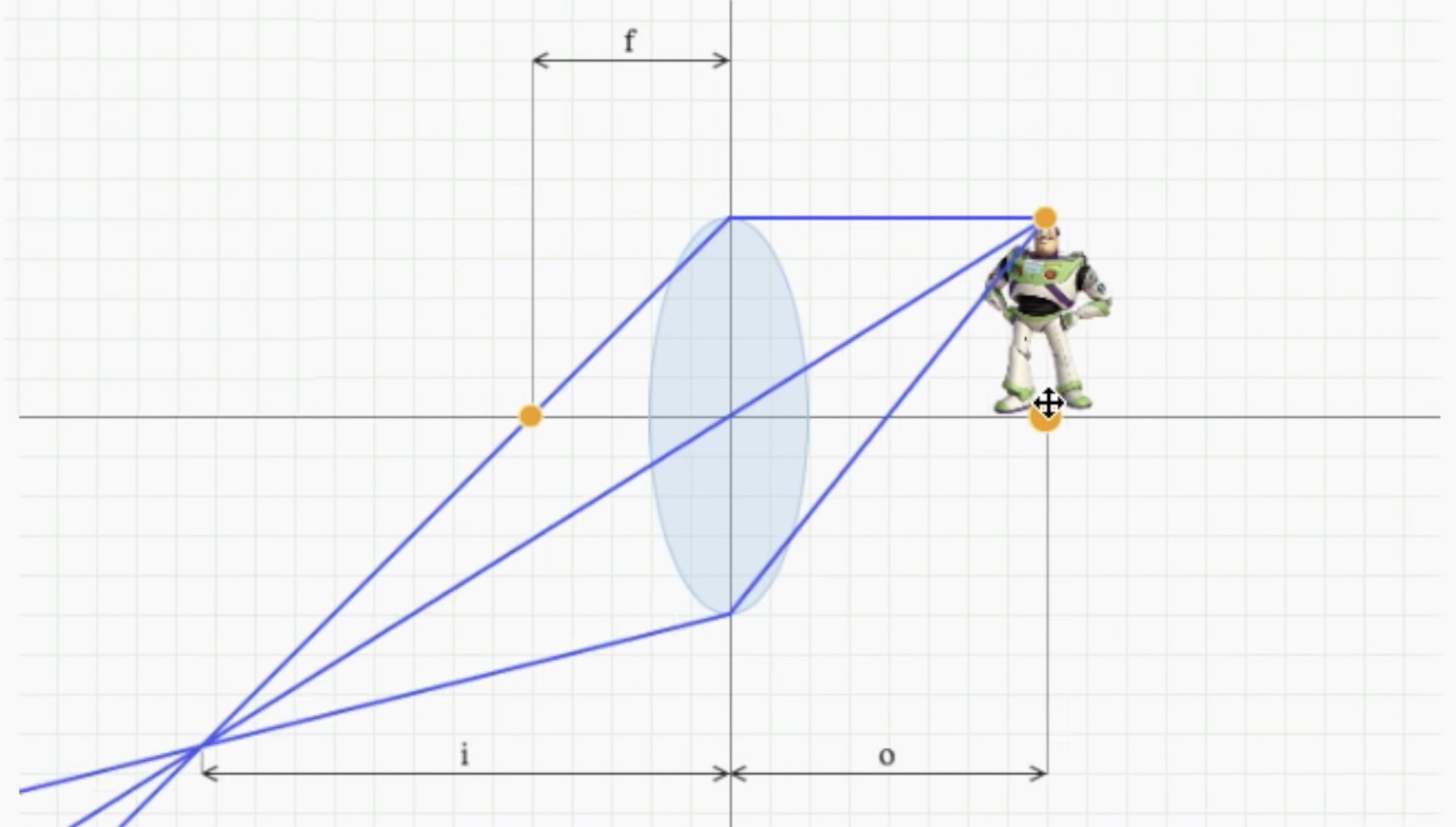
-그리고 렌즈에 o만큼 떨어진 곳에서 렌즈와 평행하게 있는 면 위에 있는 모든 점들, 그러니깐 아래 사진 상으로 렌즈에서 o만큼 떨어져있는 버즈 위치에 렌즈와 평행한 면을 놓았을 때 그 면에 있는 모든 점들은 반대쪽에 저 i 위치만큼 떨어져있는 곳에 있는 렌즈와 평행한 면에 초점이 맞춰진다는 것이다. 그래서 여길 Focus Plane이라고 부른다.
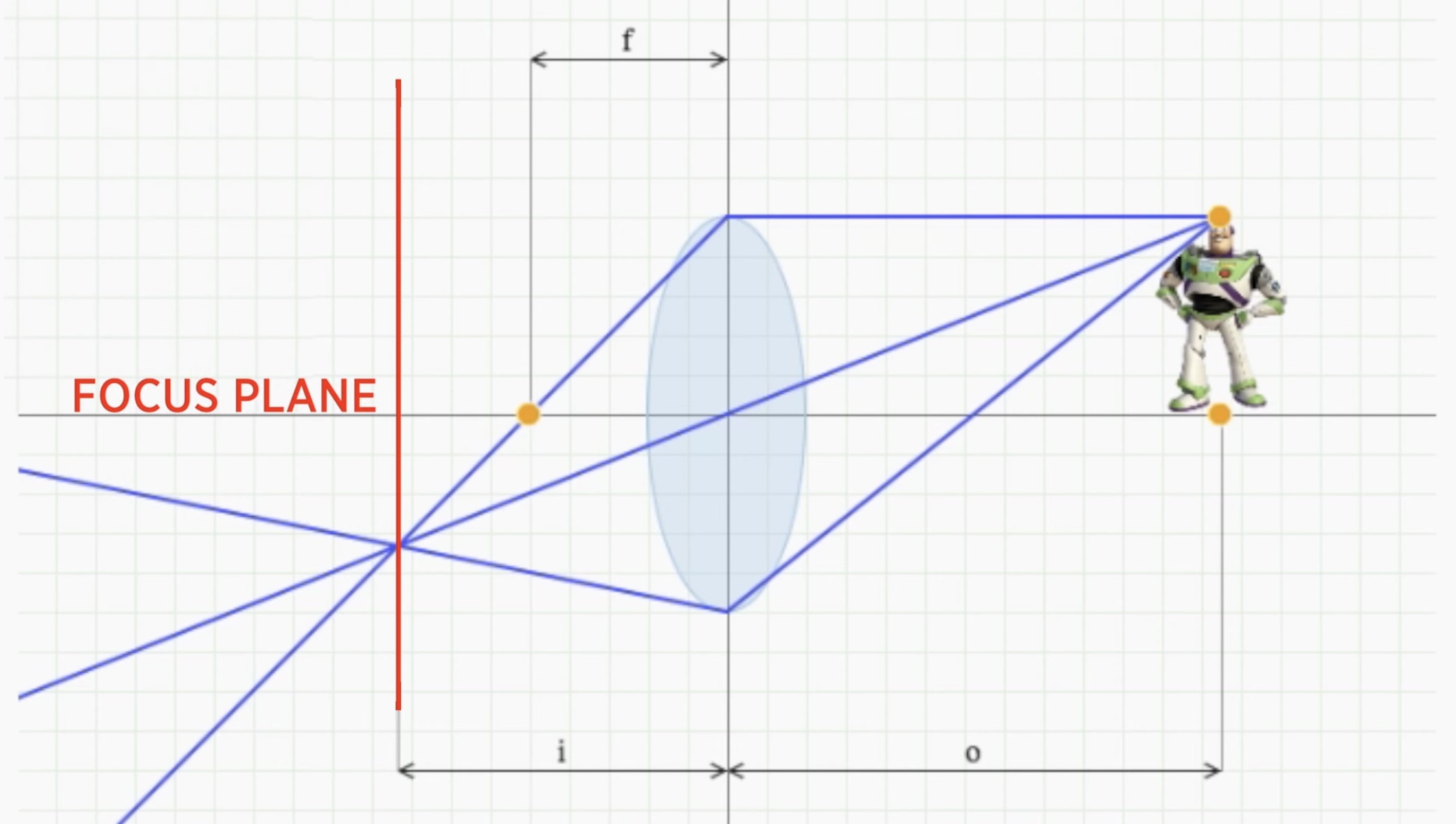
-정리하면, 렌즈에 따라 focal point(빛이 모이는 한 점)가 정해지고, 렌즈를 정했으면 focal point가 고정된다!
-그리고 focus plane은 항상 focal point의 위치에 있는게 아니다!
-focus plane의 위치는 피사체와의 거리에 따라 달라지는 것이다!
-항상 focal point에서 초점이 맞게 되는 것이 아니다! focus는 물리적인 특성일 뿐이다.
+Thin Lens Equation
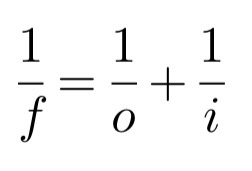
위의 저 3가지 변수들은 어떨 때 양수이고 음수인가?
*f의 양수/음수 판단
일단 f는 렌즈에서 focal point까지의 거리인 focal length이다.
focal point는 렌즈의 양쪽에 존재한다. 어느 쪽으로 할 지는 상관이 없지만 이 f가 양수인지 음수인지는 렌즈의 종류를 보면 알 수 있다.
Convex(Converging) Lens 볼록렌즈의 경우, focal length는 항상 양수이다! 렌즈의 왼쪽에 있는 focal point를 기준으로 하든 오른쪽 기준으로 하든 focal length는 항상 양수인 것이다
Concave(Diverging) Lens 오목렌즈의 경우, 반대로 초점이 양쪽 중에 어느쪽에 있던 focal length는 항상 음수이다!
*o의 양수/음수 판단
o는 렌즈에서 물체까지의 거리이다. 얘는 더 쉽다.
o는 항상 양수이다. 렌즈를 하나만 쓰는 경우에는 렌즈의 종류에 상관없이 항상 양수이다. 렌즈를 여러 개 쓰는 경우에는 음수일 수 있다.
*i의 양수/음수 판단
i는 렌즈에서부터 image까지의 거리이다. 여기서 image plane이 위치한 곳은 한국말로 상이 맺히는 곳이다. 얘는 좀 까다롭다. 렌즈를 중심으로 물체가 위치한 곳의 반대쪽에 이미지가 맺힐 때 i는 양수이다. 아니면 이렇게 생각해볼 수 있다. 렌즈를 중심으로 좌우 중에서 내 눈에 위치한 곳에 이미지가 맺히면 양수이다. 눈은 당연히 렌즈를 통과해서 물체를 보는 위치에 있겠지? 렌즈 앞 쪽에 물체를 놓고 눈으로 보면 무슨 소용이야 그렇게 볼거면 렌즈가 왜 필요해. 내 눈 앞에 물체를 먼저 놓고 그 뒤에 렌즈를 놓는 꼴이니깐. 생각해보면 눈이 어느쪽에 위치해야되는지는 쉽게 알 수 있다. 눈이 위치한 곳에 image plane이 있으면 i는 양수이다! 렌즈의 종류에 상관없다.
그럼 반대로 눈이 위치한 곳의 반대쪽에 image plane이 있으면 i는 음수이다! i의 값에 따라서 이미지가 렌즈의 양쪽 중 어느 쪽에 맺히는지도 알 수 있게 되는 것이다.
하지만 이 thin lens 방정식은 단지 가로 거리를 알려줄 뿐이지 image(상)나 물체가 얼마나 크고 작은지는 알려주지 않는다. 이걸 알고 싶으면 다른 공식을 알아야 한다.
*Magnification formula 배율 공식
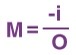
사진은 좀 구리지만 이걸로 맺힌 상의 확대/축소 비율을 알 수 있다.
-(image plane 까지의 거리 / object까지의 거리)다. 이 M의 양/음은 중요하다.
아까 o는 항상 양수라고 했다. 그래서 i가 음수이면 M은 양수고, i가 양수이면 M은 음수가 된다.
M이 양수면 상이 똑바르게 맺히고, M이 음수면 상은 거꾸로 뒤집혀서 맺힌다.
반대로 생각해서 i가 음수면 상이 똑바르게, i가 양수면 상이 거꾸로 맺힌다.

위 내용을 총정리하면 위 사진과 같다.
(참고 : https://youtu.be/7GV1UZSTNJg?si=OCZ-CI96hKjdDFWJ) 마지막 부분의 예제는 꼭 풀어보자
<Circle of Confusion (착란원)의 크기는 어떻게 되는가?>

여기서 초점이 맞지 않는 배경에서 보이는 원의 크기는 어떻게 되는가? 쉽다.
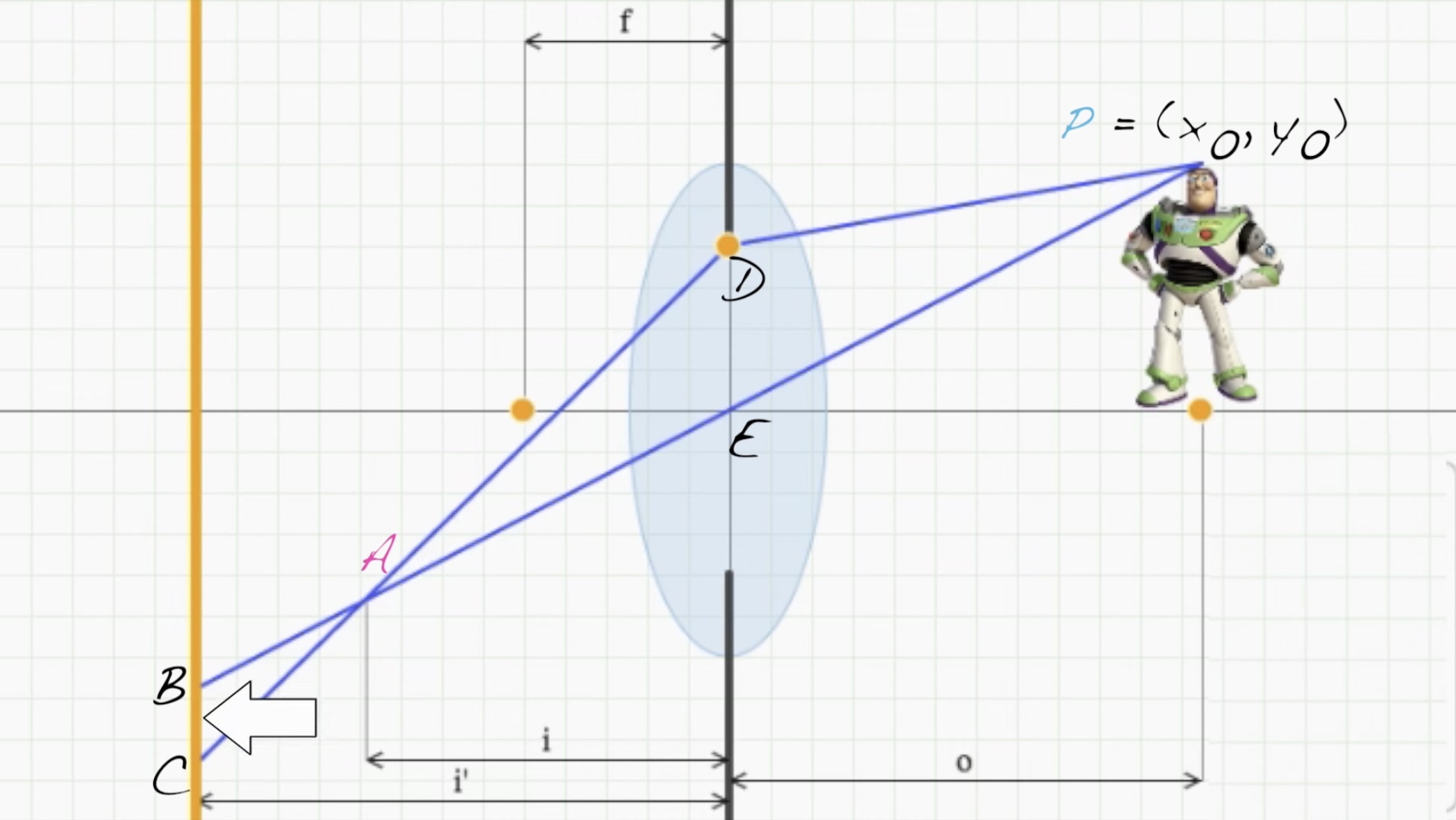
2D 상에서 봐보자. 물체에서의 한 점인 P. 그리고 P가 초점이 맞게 되는 위치인 medial ray와 parallel ray의 교차점을 A라고 하자. 렌즈의 중심을 E라고 하고 aperture의 끝을 D라고 하자. 선분 DE는 aperture의 반지름이 되는 것이다.
P에서 출발하여 선분 DE를 지나는 모든 광선은 모두 A에서 초점이 맞게 된다. 렌즈에서 A까지의 평행한 거리인 i에 image plane이 위치한다면 P는 초점이 맞게 된다.
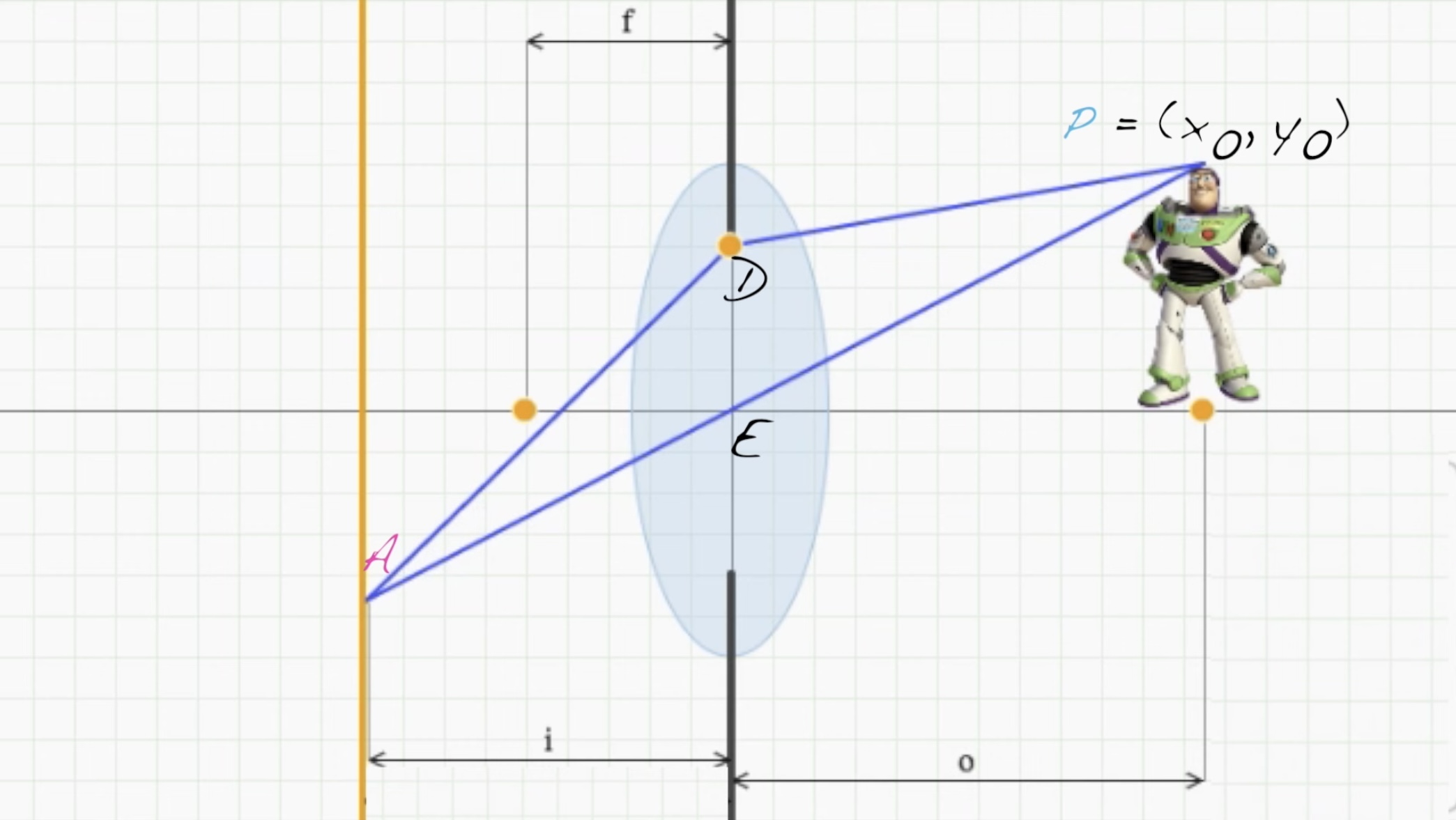
그러나 image plane이 위 그림과 같이 i보다 더 멀리 i’에 위치하게 된다면, P는 초점이 나가면서 흐려진 이미지가 BC라고 표시된 부분에 보이게 된다.
이 BC의 거리가 Circle of Confusion의 크기이다! 선분 BC가 blur의 반지름인 것이다!